$NetworkX$追加課題

サーバー負荷を軽減させるため，大きなグラフを描画しないこと．

$11/6$実施の$NetworkX$課題で規定点に満たしていない者が提出するものである．

また，提出する必要のない人でも，自学自習のために利用しても良い．

基本的に，これらの問題は以下のURLの動画を参照し作成したため，動画を視聴しつつ解くことをおすすめする．
詳しく知りたい人向けに参考資料のリンクも置いておくので，必要のある人は参考にしてください．
応用プログラミング演習では，最適化を行う際この$NetworkX$を利用する可能性があるため，基本操作を出来るようになっていてください．

参考動画：https://www.youtube.com/watch?v=YrkfcVlr_bA&feature=youtu.be

この動画中に出てくるスライドのコードを打つことが今回の追加課題とする．

参考資料：http://www.logopt.com/python_learning/wp-content/uploads/2015/01/networkx.pdf

小テストの点で成績を付けるため単位認定を目指すならば，一番下の加点課題を解いたほうが吉

1. 無向グラフを作成し，点と枝を表示せよ．


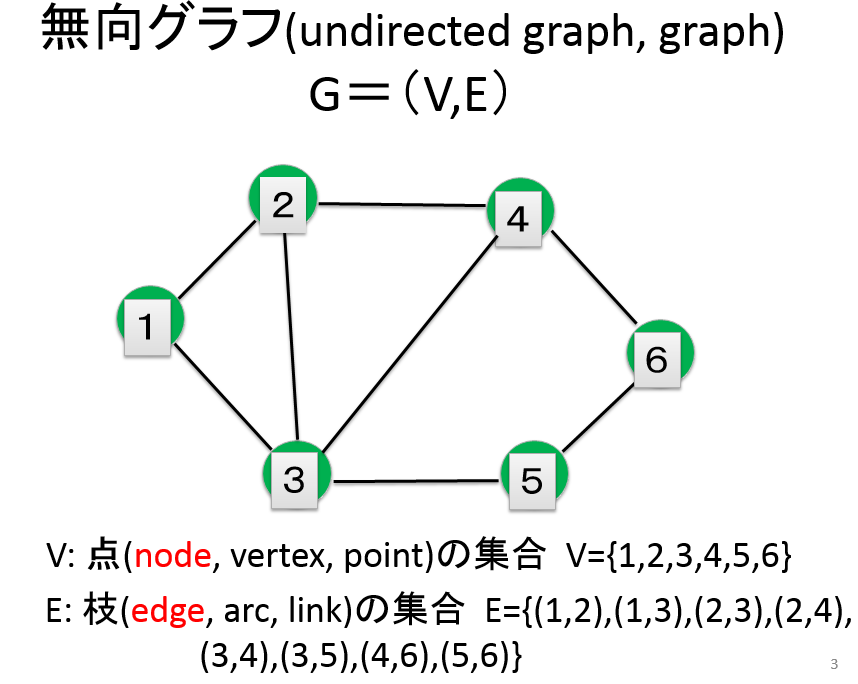
グラフを作成した後に$print$を用いてグラフに含まれる点と枝を列挙せよ．

In [ ]:

2. 有向グラフを作成し，点と枝を表示せよ．


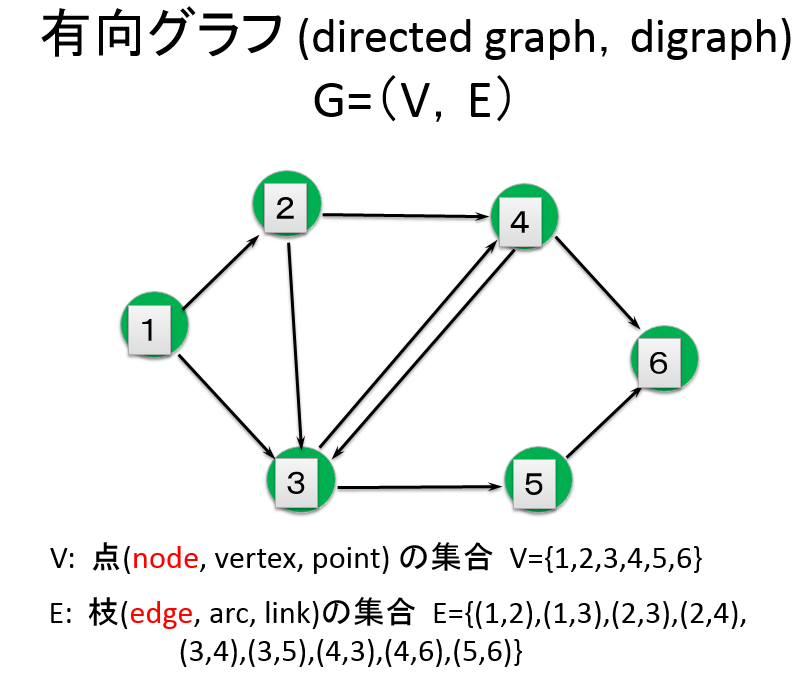
グラフを作成した後に$print$を用いてグラフに含まれる点と枝を列挙せよ．

In [ ]:

3. 属性が付与された有向グラフを作成し，点と枝を表示せよ．


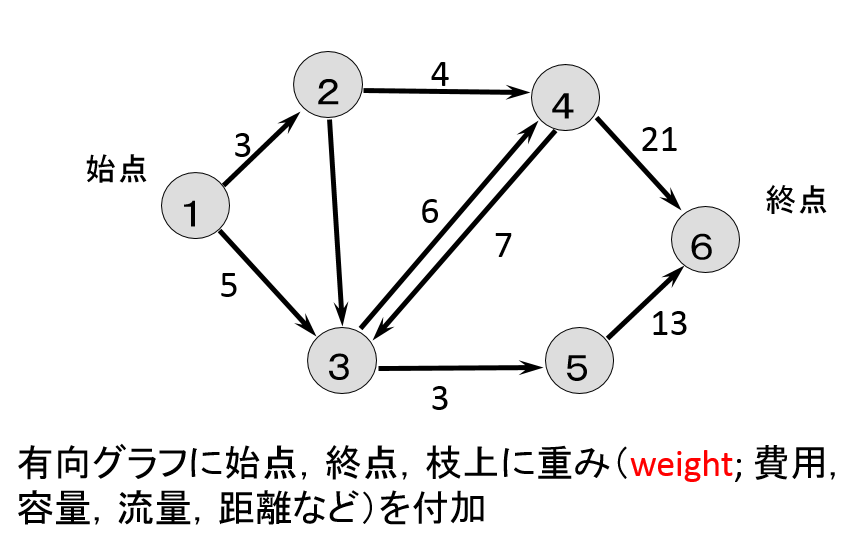
グラフを作成した後に$print$を用いてグラフに含まれる点と枝を列挙せよ．

In [ ]:

4.参考動画のスライド10からスライド13までのコードをスライド毎に点と枝を表示するように実行せよ．

但し，スライド毎にグラフを定義するのではなく，スライド10で定義し，そのグラフを11,12,13でも順に用いること．

In [ ]:
###10
In [ ]:
###11
In [ ]:
###12
In [ ]:
###13

5.スライド14の右下にあるグラフを実装し，コードを実行せよ．

In [ ]:
###14

6.スライド15,16,17を実行せよ．

In [ ]:
###15
In [ ]:
###16
In [ ]:
###17

7.グラフ描画をするコードを打ち，スライド20のグラフを描画し，21を実行せよ

但し$import$文はコメントアウトし（半角シャープ）$Jupyter$上なので$inline$表示するコードを実装せよ

In [ ]:
### 描画コード

###20
In [ ]:
###21

8.以下の指定したスライドのコードを実行せよ

In [ ]:
###27
In [ ]:
###29
In [ ]:
###30
In [ ]:
###31
In [ ]:
###32
In [ ]:
###33
In [ ]:
###34
In [ ]:
###35
In [ ]:
###36
In [ ]:
###37
In [ ]:
###38
In [ ]:
###42
In [ ]:
###43
In [ ]:
###48
In [ ]:
###50
In [ ]:
###51

加点課題 1

問1 山手線と中央線と丸ノ内線の駅名をノードとしたグラフを生成せよ（ノード名はローマ字）

但し，サーバーに対する負荷を軽減するため，以下の制約の元実行せよ．

  • $山手線：新宿，池袋，田端，渋谷，品川，東京$
  • $中央線：新宿～東京の区間$
  • $丸ノ内線：新宿，四谷，霞が関，東京$
In [ ]:

問2 緯度経度を参照し，位置情報を与え，描画せよ

参考URL：http://www.odekakemap.com/station/

但し，緯度の数値は2倍したものを入れよ

In [ ]:

問3 緯度経度から駅間のユークリッド距離を計算し，その距離を枝の重さにしてダイクストラ法を用いて池袋駅から東京駅までの最短路を求めよ．

In [ ]:

加点課題 2

問 Twitterにおける相互フォロー間の会話

Twitterは，自分の投稿と予め「フォロー」をしたユーザーの投稿が見えるものである．
以下のテキストデータは，前者が後者をフォローしていることを表している．（上から順に，AさんがBさんをフォローしている，AさんがCさんをフォローしている…）
まずは，以下のテキストデータを読み込み，相互フォローをしている人たちのネットワークを構成し，そのグラフの枝をprintせよ．
$Hint:$前者，後者両方から枝を伸びているものを抽出する

"""A,B A,C A,D A,E A,F B,A B,C B,D B,F C,A C,B C,D C,E D,A D,B D,C D,E D,F E,A E,B F,C F,D G,A G,D """
In [ ]:

問2． 最大安定集合の値を求めるプログラムを書け．

この値が相互フォローを行っている人達の最大の集合であり，リプライを送らなくとも会話が可能な人達の人数である．
通称：空リプ

In [ ]:

問3． 最大安定集合の値を持つ組み合わせを全て列挙するプログラムを書け．

In [ ]: