実務的な需要予測手法
量的な予測手法の分類
予測は大きく質的な予測と量的な予測に分けられる.ここでは,量的な予測に限定して話を進める.量的予測手法は,大きく分けて時系列モデルと回帰モデルに分類できる.
時系列モデル
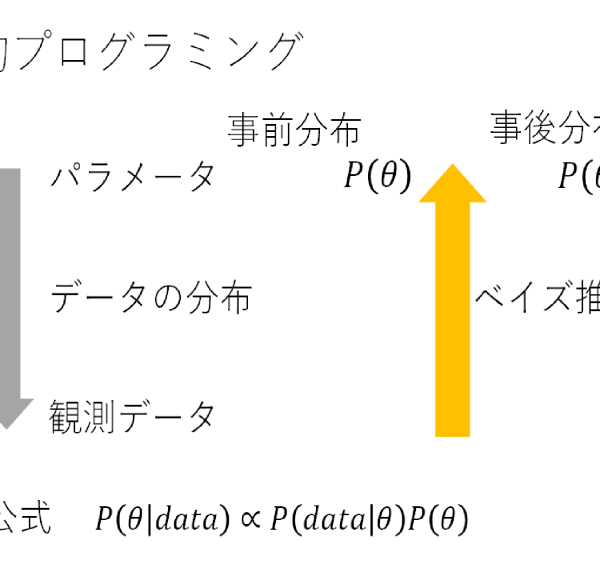
時系列予測は,時系列データが主で,付随するデータが少量のものを指す.ARIMAや指数平滑法などの古典的な手法や,確率的プログラミングに基づく手法が含まれる.指数平滑法には,傾向変動を考慮したHolt法や周期的な変動を考慮したHolt-Winter法があり,大規模データで高速に計算したい場合にはこれらが推奨される.計算量はかかるが,より精度を高めた予測が必要な場合には,ベイズ推論に基づく確率的プログラミングアプローチが推奨される.
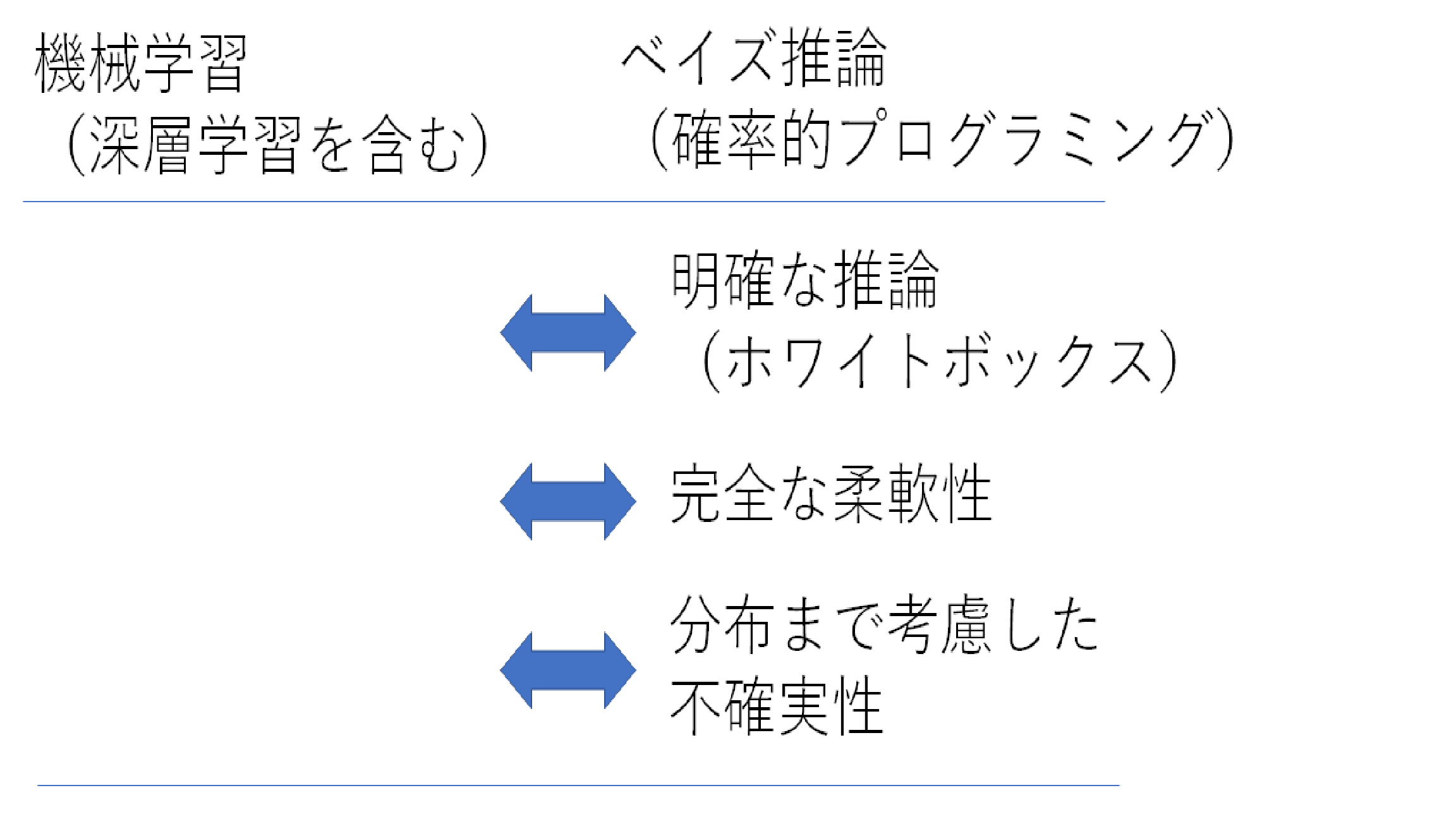
右図に示すように,確率的プログラミングに基づく手法は,明確な推論,完全な柔軟性,分布までを考慮した不確実性を扱えるものである.それに対して機械(深層)学習は,推論が不明確,柔軟性がない,分布が扱えないという批判もある(がそれも以下で述べるように,使い方次第である).
回帰モデル
回帰モデルにはランダム森に代表される機械学習アルゴリズムと,ニューラルネットを用いた深層学習がある.
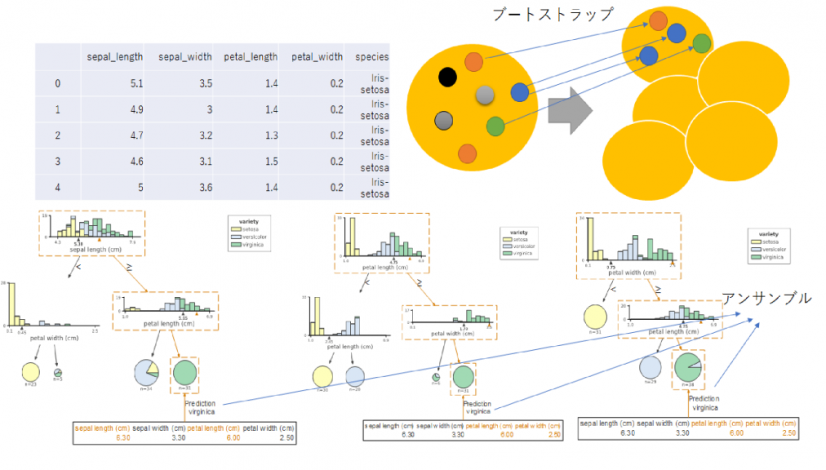
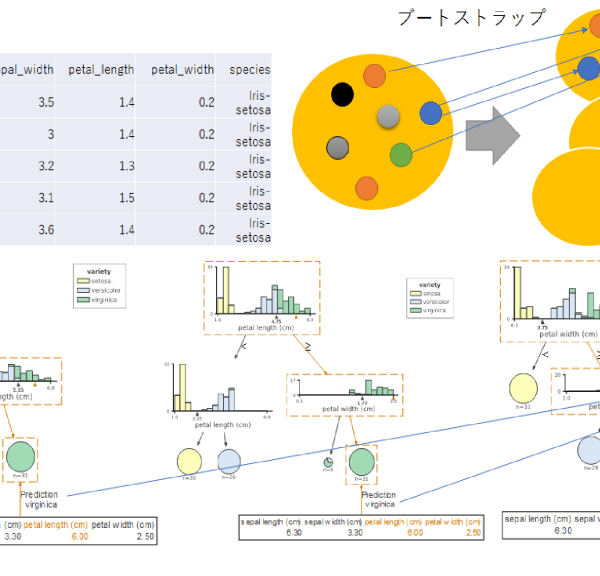
上の3番目の図に示したのがランダム森である.簡単に言うとブーストラップによって抽出したランダムデータに対して,ランダムに選択した特徴による森(決定木)を作成し,それらのアンサンブル(多数決)によって予測を行う手法である.
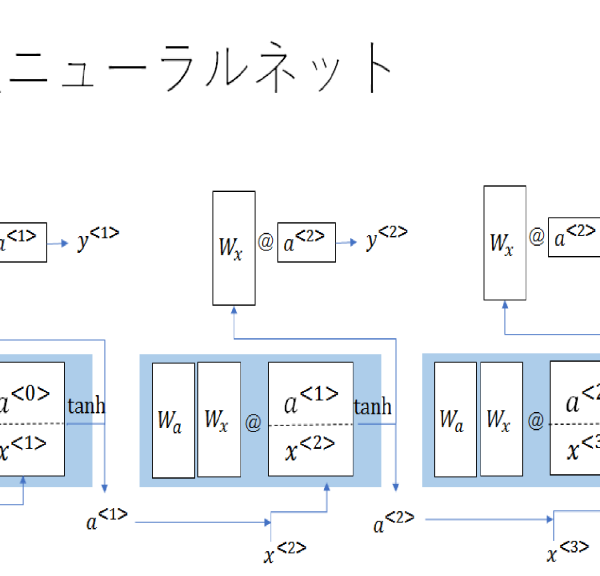
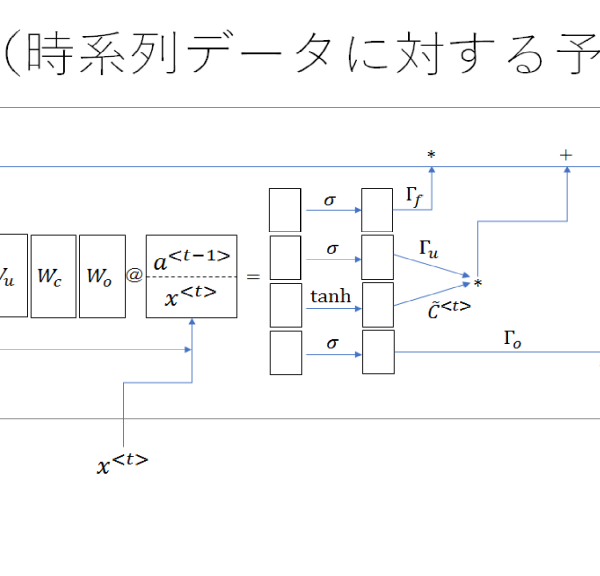
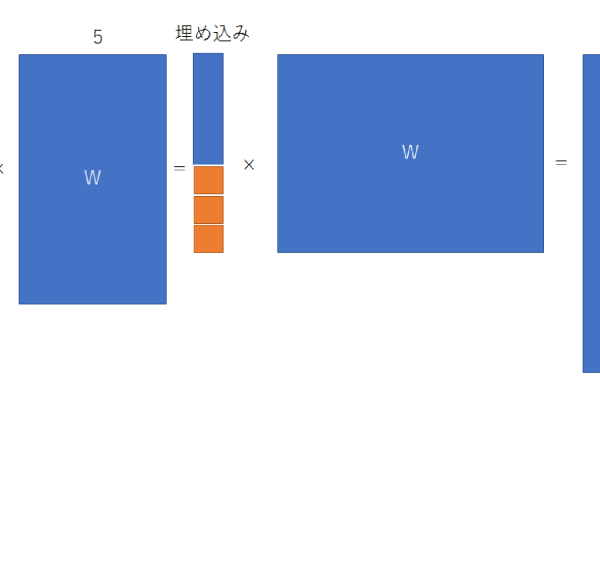
一方,4番目の図に示したのは,時系列データに対する回帰型ニューラルネットであり,実務的には5番目に示したLSTMアークテクチャを用いる方が良い.しかし,我々が実務でよく使うのは,6番目に示した埋め込み層を用いたニューラルネットである.これは,日付データを多くの特徴に分解し,カテゴリーデータとし,それを埋め込み層によって処理をする手法である.
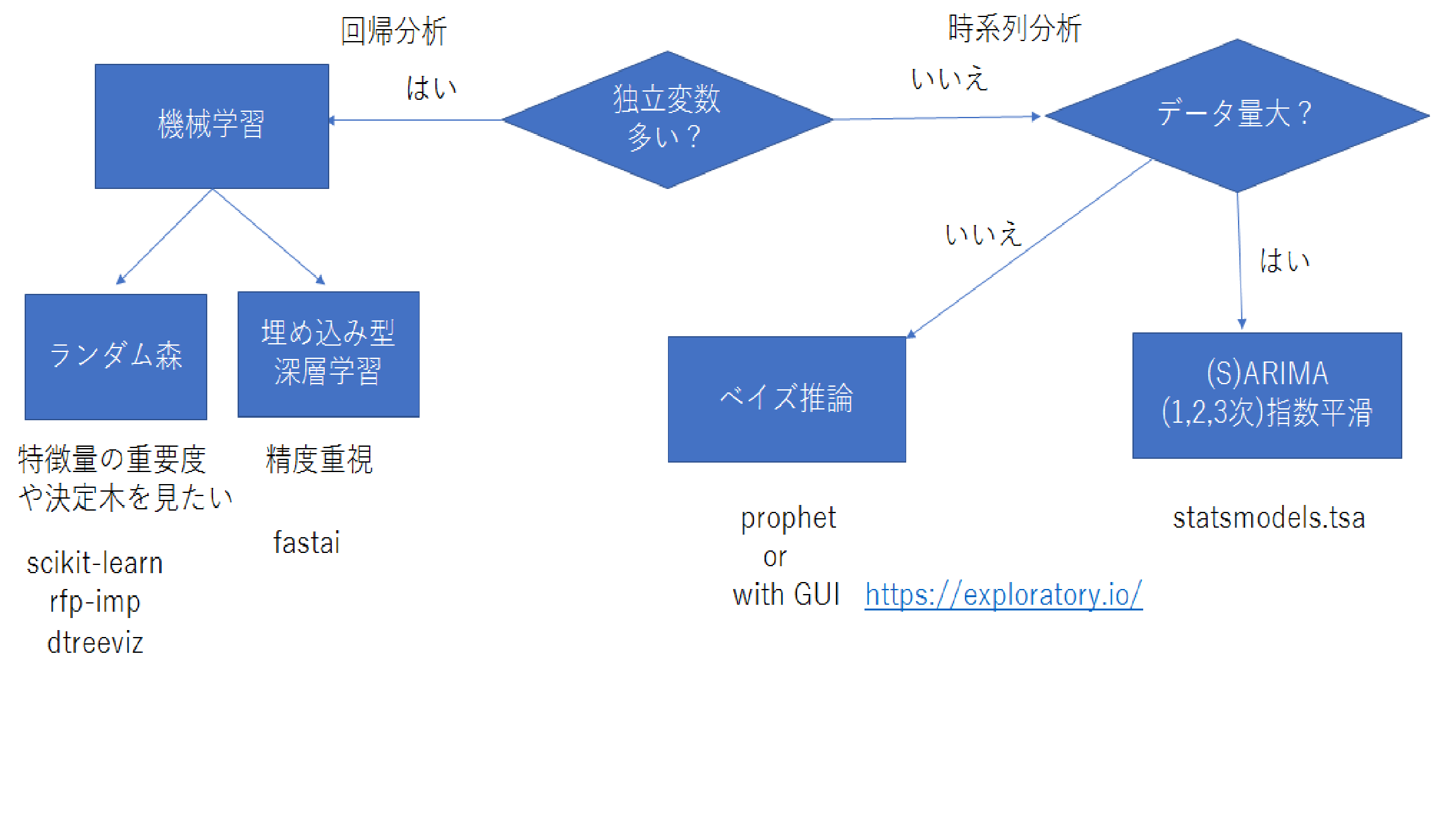
これらの手法の使い分けを以下の図に示した.いずれも無料(一部有料)のライブラリによって簡単に使うことができる.